Answer:
C
Explanation:
To find the inverse, let y = f(x) then rearrange making x the subject, that is
y = 5(x + 3)³ - 2 ( add 2 to both sides )
y + 2 = 5(x + 3)³ ( divide both sides by 5 )
(x + 3)³ =
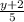
Take the cube root of both sides
x + 3 =
![\sqrt[3]{(y+2)/(5) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/ywqyn4raarn5ck68vns7n7vxfyem4fvmie.png)
Subtract 3 from both sides
x =
![\sqrt[3]{(y+2)/(5) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/ywqyn4raarn5ck68vns7n7vxfyem4fvmie.png) - 3
- 3
Change y back into terms of x, so
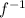 (x ) =
(x ) =
![\sqrt[3]{(x+2)/(5) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/ckgdxxxiw1t3dnggxugyhoytm63ccj6dta.png) - 3 → C
- 3 → C