Answer:
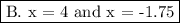
Explanation:
ƒ(x) = x² - 2x – 8; g(x) = ¼x -1
If ƒ(x) = g(x), then
x² - 2x – 8 = ¼x -1
One way to solve this problem is by completing the square.
Step 1. Subtract ¼ x from each side
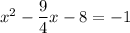
Step 2. Move the constant term to the other side of the equation
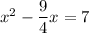
Step 3. Complete the square on the left-hand side
Take half the coefficient of x, square it, and add it to each side of the equation.
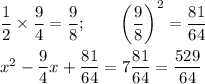
Step 4. Write the left-hand side as a perfect square
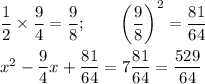
Step 5. Take the square root of each side
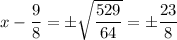
Step 6. Solve for x
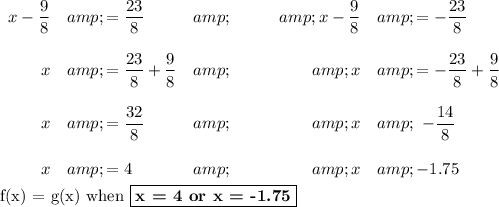
Check:
![\begin{array}{rlcrl}4^(2) - 2(4) - 8 & = (1)/(4)(4) -1&\qquad & (-1.75)^(2) - 2(-1.75) - 8 & = (1)/(4)(-1.75) - 1\\\\16 - 8 -8& = 1 - 1&\qquad & 3.0625 +3.5 - 8 & = -0.4375 - 1 \\\\0& =0&\qquad & -1.4375 & = -1.4375 \\\\\end{array}]()
The diagram below shows that the graph of g(x) intersects that of the parabola ƒ(x) at x = -1.7 and x = 4.