Question

Please help asap!!!!!!!!!!!

Answer 1

Hello!

The answer is:

The correct option is the second option:

`SectorArea=8\pi in^(2)`

Why?

To answer the question, we need to calculate the total area of the circle (which corresponds to 360°) and then, calculate the equivalent area to the sector of the arc that measures 45°

Calculating the total area, we have:

`TotalArea=\pi radius^(2) \\\\TotalArea=\pi 8^(2) =64\pi in^(2)`

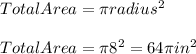
Now, we need to consider that the calculated area (total area) correspondes to all 360° that conforms the interior angle of a circle, now, if we want to calculate the area that represents a sector of the arc that measures 45°, we have to use the following formula:

`SectorArea=(360\°)/(45\° )*TotalArea\\\\SectorArea=(45\°)/(360\° )*64\pi in^(2)=(1)/(8) *64\pi in^(2)\\\\SectorArea=8\pi in^(2)`

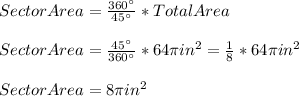
Hence, we have that the correct option is the second option:

`SectorArea=8\pi in^(2)`

Have a nice day!

Answer 2

`16\pi \: sq.in`

Step-by-step explanation

The area of a sector is calculated using the formula,

`Area = (arc \: measure)/(360 \degree) * \pi {r}^(2)`

The arc measure is given as 45°

The radius of the circle is 8 inches.

We substitute to obtain,

`Area = (45 \degree)/(360 \degree) * \pi * {8}^(2)`

`Area = (1)/(4) * 64\pi = 16\pi`