Answer:
The solution for k is the interval (-3.5,1.5)
Explanation:
we have
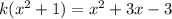
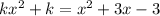
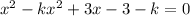
![}[1-k]x^(2)+3x-(3+k)=0](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wqx6v1fdsopo8brmsy9k7xxk8c4yckwc4q.png)
we know that
If the discriminant is greater than zero . then the quadratic equation has two real and distinct solutions
The discriminant is equal to
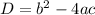
In this problem we have
a=(1-k)
b=3
c=-(3+k)
substitute
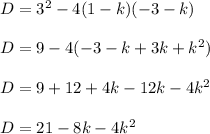
so
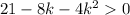
solve the quadratic equation by graphing
The solution for k is the interval (-3.5,1.5)
see the attached figure