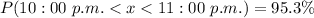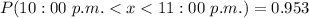Question

Flight 202's arrival time is normally distributed with a mean arrival time of 10:30 p.m. and a standard deviation of 15 minutes. Use the eight-part symmetry of the area under a normal curve to find the probability that a randomly chosen arrival time is between 10:00 p.m. and 11:00 p.m.

The probability is__

Answer 1

The probability is 0.953

Explanation:

We know that the mean
`\mu` is:

`\mu=10:30\ p.m`

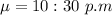
The standard deviation
`\sigma` is:

`\sigma=0:15\ minutes`

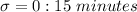
The Z-score is:

`Z=(x-\mu)/(\sigma)`

We seek to find

`P(10:00\ p.m.<x<11:00\ p.m.)`

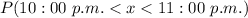
The Z-score is:

`Z=(x-\mu)/(\sigma)`

`Z=(10:00-10:30)/(0:15)`

`Z=(-0:30)/(0:15)`

`Z=-2`

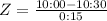
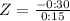
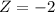
The score of Z =-2 means that 10:00 p.m. is -2 standard deviations from the mean. Then by the rule of the 8 parts of the normal curve, the area that satisfies the condition of 2 deviations from the mean has percentage of 2.35%

and

`Z=(x-\mu)/(\sigma)`

`Z=(11:00-10:30)/(0:15)`

`Z=(0:30)/(0:15)`

`Z=2`

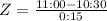
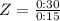
The score of Z =2 means that 11:00 p.m. is 2 standard deviations from the mean. Then by the rule of the 8 parts of the normal curve, the area that satisfies the condition of 2 deviations from the mean has percentage of 2.35%

`P(10:00\ p.m.<x<11:00\ p.m.)=100\%-2.35\%-2.35\%`

`P(10:00\ p.m.<x<11:00\ p.m.)=95.3\%`

`P(10:00\ p.m.<x<11:00\ p.m.)=0.953`