Answer:
Angle 1 = 108°
Angle 2 = 72°
Angle 3 = 120°
Angle 4 = 96°
Angle 5 = 144°
Explanation:
We need to find the measures of the interior angles in a pentagon if the measure of each consecutive angle is in the ratio 9:6:10:8:12.
Let x be the common ratio
So, we can write:
Angle 1 = 9x
Angle 2 = 6x
Angle 3 = 10x
Angle 4 = 8x
Angle 5 = 12x
We know that the sum of all angles of pentagon = 540
So, adding all angles and equal them to 540, we can find value of x
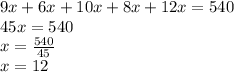
So, we get the value of x: x=12
Now, calculating the angles by putting x=12:
Angle 1 = 9x = 9(12) = 108°
Angle 2 = 6x = 6(12) = 72°
Angle 3 = 10x = 10(12) = 120°
Angle 4 = 8x = 8(12) = 96°
Angle 5 = 12x= 12(12) = 144°