Question

Solve the system of equations given below

Answer 1

`</p><p>y-15=3x \\</p><p>-2x+5y=-3 \\ \\</p><p>-2x+y-15=0 /\cdot2 \\</p><p>-2x+5y-3=0 /\cdot(-2) \\ \\</p><p>-4x+2y-30=0 \\</p><p>4x-10y+6=0 \\ \\</p><p>-8y-24=0 \\</p><p>\boxed{y=-3} \\ \\</p><p>-3-15=3x \\</p><p>\boxed{x=-6}</p><p>`

The answer is C. (-6, -3)

Hope this helps.

r3t40

Answer 2

For this case we have the following system of equations:

`y-15 = 3x\\-2x + 5y = -3`

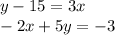
We multiply the first equation by -5:

`-5y + 75 = -15x`

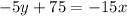
Now we add the equations:

`-2x-5y + 5y + 75 = -3-15x\\-2x + 75 = -3-15x\\-2x + 15x = -75-3\\13x = -78\\x = \frac {-78} {13}\\x = -6`

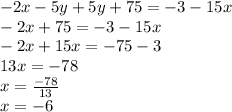
We find the value of the variable "y" according to the first equation:

`y = 3x + 15\\y = 3 (-6) +15\\y = -18 + 15\\y = -3`

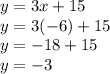
The solution of the system is: (-6, -3)

Answer:

(-6, -3)

Option C