Hello!
The answer is:
The equation of the line that it's parallalel to the given line and passes through the point (-6,-1) will be:
A.
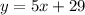
Why?
To find an equation in slope-intercept form for the linea paralallel to the given line, we must guarantee that the new line will have the same slope of the given line.
We are given the line:
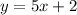
Where its slope is equal to 5
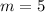
and the point (-6,-1)
The slopte-intercept form of a line, is given by the following equation:
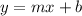
Then, we know that the line that we are looking for, will have a slope equal to 5, so:
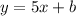
Now, substituting the given point in order to find "b", we have:
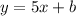
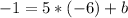
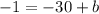
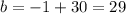
Hence, we have that the equation of the line that it's parallalel to the given line and passes through the point (-6,-1) will be:
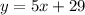
Have a nice day!