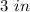For this case we have by definition, that a hemisphere represents half of a sphere.
Its volume is given by:
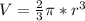
Where "r" represents the radius.
Substituting the data and clearing the radio we have:
![\frac {2} {3} \pi * r ^ 3 = 18 \pi\\\frac {2} {3} * r ^ 3 = 18\\r ^ 3 = 18 * \frac {3} {2}\\r ^ 3 = 27\\r = \sqrt [3] {27}\\r = 3](https://img.qammunity.org/2020/formulas/mathematics/high-school/m0u3qyjq2jpbsqi3nt9wctz2pbfa68aop4.png)
Thus, the radius of the hemisphere is 3 inches.
Answer: