Question

Given: circle k(O), m LM = 164°, m WK = 68°, m∠MLK = 65° . Find: m∠LMW

Answer 1

The measure of angle LMW is

`m\angle LMW=67\°`

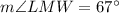
Explanation:

see the attached figure to better understand the problem

step 1

Find the measure of arc MW

we know that

The inscribed angle measures half that of the arc comprising

so

`m\angle MLK=(1)/(2)[arc\ MW+arc\ WK]`

substitute the given values

`65\°=(1)/(2)[arc\ MW+68\°]\\ 130\°=[arc\ MW+68\°]\\ arc\ MW=130\°-68\°=62\°`

step 2

Find the measure of arc LK

we know that

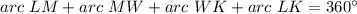`arc\ LM+arc\ MW+arc\ WK+arc\ LK=360\°` -----> by complete circle

substitute the given values

`164\°+62\°+68\°+arc\ LK=360\°\\ 294\°+arc\ LK=360\°\\ arc\ LK=360\°-294\°=66\°`

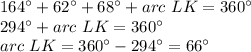
step 3

Find the measure of angle LMW

we know that

The inscribed angle measures half that of the arc comprising

so

`m\angle LMW=(1)/(2)[arc\ LK+arc\ WK]`

substitute the given values

`m\angle LMW=(1)/(2)[66\°+68\°]=67\°`