Question

Help me!!!!!! I’ll been stuck on this for to long

Answer 1

The distribution is very simple. Using FOIL.

It states that
`(a+b)(c+d)=ac+ad+bc+bd`.

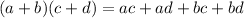Also note that when multiplying expressions we multiply variables and values differently. If we have variables like
`x` their exponents will add. If we have values like 3 we multiply them normally.

For example your practise 3.

`(x+3)(2x^2+4)=2x^2\cdot x+4x+3\cdot2x^2+3\cdot4 \\</p><p>\underline{2x^3+4x+6x^2+12}</p><p>`

Now just order the expressions from bigger exponent to smaller and than values. (Usual notation although no need).

And solution is:

`\boxed{2x^3+6x^2+4x+12}`

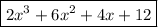
Hope this helps.

r3t40

Answer 2

See below

Explanation:

`a\cdot(b + c) = a\cdot b + a\cdot c`

3) Practice: Organizing information

`\begin{array}{lll}\qquad \textbf{Steps} & \textbf{Problem: }(x + 3)(2x^(2) + 4) & \\\textbf{1. List variables} & a = x + 3 & \\ & b = 2x^(2) & \\ & c = 4 &\\\\\textbf{2. Distribute} & (x + 3)(2x^(2) + 4)& = (x + 3)(2x^(2)) + (x + 3)(4)\\\\\textbf{3. Redistribute} & (x + 3)(2x^(2))& (x + 3)(4)\\& a = 2x^(2) & a = 4\\& b = x & b = x\\& c = 3 & c = 3\\& 2x^(3) + 6x^(2) & 4x + 12\\\textbf{4. Combine}& & \\\qquad\textbf{terms} & 2x^(3) + 6x^(2)+ 4x + 12 & \\\end{array}`

4. Practice: Summarizing

`\text{You can use the FOIL method to multiply two }\underline{\text{binomials}}.\\\text{The letters in FOIL stand for }\underline{\text{First, Outer, Inner, Last}}.\\\text{The FOIL method helps you to remember how to multiply each term in one }\\\underline{\text{binomial}} \text{ by each term in the other }\underline{\text{binomial}}.`