Question

The diagonals of a parallelogram are 24 meters and 40 meters and intersect at an angle of 60º. find the length of the longer side.

Answer 1

The length of the longer side is 28 meters

Explanation:

we know that

In a parallelogram, the intersecting diagonals bisect each other;

The supplementary angle of 60° is 120°.

see the attached figure to better understand the problem

Let

a ----> the length of the longer side

b ----> the length of the shorter side.

Apply the Law of Cosines to the lower triangle.

`a^2 = 20^2 + 12^2 - 2(20)(12) cos(120\°)`

`a^2 = 784`

`a=28\ m`

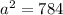
therefore

The length of the longer side is 28 meters