Hello!
The answer is:
The correct option is:
B)
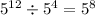
Why?
To solve the problem, we need to remember the quotient of power property, it's defined by the following relation:
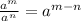
If we have a quotienf of powers that have the same base, we need to keep the same base and subtract the exponent of the denominator power to the exponent of the numerator power.
So, we are given the expression:
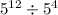
Which is equal to write:
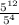
Then, calculating we have:
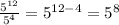
Hence, the answer is:
B)

or
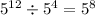
Have a nice day!