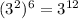Hello!
The answer is:
The correct option is:
D)
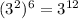
Why?
To solve the problem, we need to remember the power of a power property, it's defined by the following way:
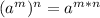
When we have a power of a power, we must keep the base and then, the new exponent will be the product between the two original exponents.
So, we are given the expression:
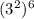
Then, calculating we have:
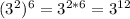
Hence, we have that the correct option is:
D)