Answer:
The value of x is 62
Explanation:
Given data is:
34,37,53,55,x,x+2,77,83,89and100
As the number of values is 10 (which is even number of values) i.e. n=10
The median will be the average of two middle values.
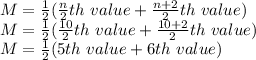
As it is already given that the median is 63
Putting M=63
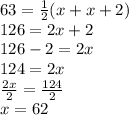
Hence,
The value of x is 62