Answer:
Mix 50 mL of the 68% solution with 40 mL of the 77% solution to make 90 mL of the 72% solution.
Step-by-step explanation:
Let the volume required of the 68% solution be
 mL. The volume of the 68% solution and the 77% solution shall add up to 90 mL. Thus the volume required of the 77% solution shall be
mL. The volume of the 68% solution and the 77% solution shall add up to 90 mL. Thus the volume required of the 77% solution shall be
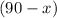 mL.
mL.
The amount of solute in the 72% solution will be:
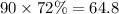 .
.
The
 mL of the 68% solution will contribute:
mL of the 68% solution will contribute:
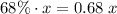 .
.
The
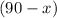 mL of the 77% solution will contribute:
mL of the 77% solution will contribute:
 .
.
The two values shall add up to
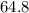 . That is:
. That is:
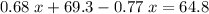 .
.
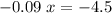 .
.
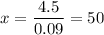 .
.
In other words, there need to be
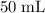 of the 68% solution, and
of the 68% solution, and
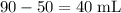 of the 77% solution.
of the 77% solution.