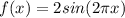Answer: Third option.
Explanation:
We know that the sine function is:
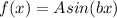
Where "A" is the amplitude of the function( This is half the vertical distance between minimum value and maximum value of the function) and
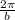 is the period.
is the period.
Observe in the graph that the amplitude is:
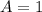
And the period is 1, then "b" is:
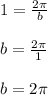
Then the function shown in the graph is:
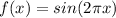
By definition in the transformation of the function:
When
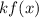 and
and
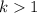 then the function is stretched vertically by a factor of "k".
then the function is stretched vertically by a factor of "k".
In this case we know that the function shown in the graph is vertically stretched by a factor of 2 to produce a new graph. Then:
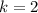
Therefore,the function that represents the new graph is: