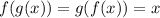Question

Consider the two functions shown below.

Answer 1

Answer: Option B

Then The functions f(x) and g(x) are inverses because
`f(g(x))=g(f(x))=x`

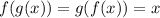
Explanation:

To answer this question we must make the composition of f (x) and g (x)

We found

`f (g(x))`

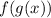
We know that

`f(x) = 2x-2\\\\g(x) = (1)/(2)x + 1`

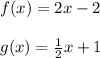
By definition if two functions f and g are inverses then it follows that:

`f(g(x)) = g(f(x)) = x`

So if
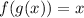`f(g(x)) = x` f and g are inverse

To find
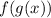`f(g(x))` enter the function g(x) within the function f(x) as shown below

`f(g(x))= 2( (1)/(2)x + 1)-2\\\\f(g(x))= x + 2 -2\\\\f(g(x))= x`

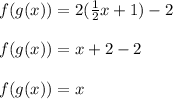
Now

`g(f(x))= (1)/(2)(2x-2) + 1\\\\g(f(x))= x-1 + 1\\\\g(f(x))= x`

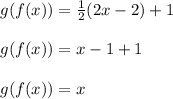
Observe that

`f(g(x))=g(f(x))=x`

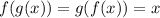
Then The functions f(x) and g(x) are inverses because
`f(g(x))=g(f(x))=x`

Answer 2

B. The functions f(x) and g(x) because f(g(x))=g(f(x))=x

EXPLANATION

The given functions are:

`f(x) = 2x - 2`

and

`g(x) = (1)/(2)x + 1`

If f(x) and g(x) are inverses, then

f(g(x))=x

`f(g(x))=f( (1)/(2) x + 1)`

`f(g(x))=2( (1)/(2)x + 1) - 2`

Expand the parenthesis to obtain,

`f(g(x))=x + 2- 2`

`f(g(x))=x`

Also,

`g(f(x)) = g(2x - 2)`

`g(f(x)) = (1)/(2) (2x - 2) + 1`

`g(f(x)) = x - 1+ 1`

`g(f(x)) = x`

Hence f(x) and g(x) are inverses