(Tn) is an arithmetic sequence in which T3-T5=6, T4= 16 , find the (n)th term and find the order and the value of the first negative term in this sequence . Please help

Question

asked Sep 18, 2020 115k views

1 Answer

WhatsTheDiff · Answer 1 · 2020-09-23T13:44:05+0000

Since
T_n is arithmetic, it's given recursively by

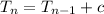
T_n=T_(n-1)+c

where
is a fixed number and
T_1 is the starting term in the sequence. We have

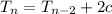
T_n=T_(n-2)+2c

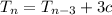
T_n=T_(n-3)+3c

and so on, so that

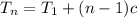
T_n=T_1+(n-1)c

We're told that
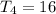T_4=16 , so

16=T_3+c

and

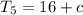
T_5=16+c

so that

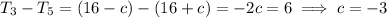
$T_3-T_5=(16-c)-(16+c)=-2c=6\implies c=-3$

Then the first term in the sequence is
T_1 :

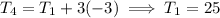
$T_4=T_1+3(-3)\implies T_1=25$

and the sequence has general formula

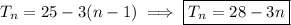
$T_n=25-3(n-1)\implies\boxed{T_n=28-3n}$

The first negative term occurs for

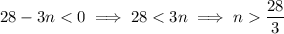
$28-3n<0\implies28<3n\implies n>\frac{28}3$

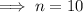
$\implies n=10$

The first negative term in the sequence is
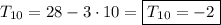$T_(10)=28-3\cdot10=\boxed{T_(10)=-2}$ .