Question

Emma and Kyle combine their eamings to pay their

bills. Emma's eamings can be modeled by the
equation E(x) = 22.75x + 74, where x is the number
of hours worked in a week. Kyle's eamings are
modeled by the equation K(x) = 17 85x + 127, where
x is the number of hours if they each work the same
number of hours in a week?
a. C(x) = 241.60x
b. Cix) = 40,60x + 201
c.Cix) = 40.60x + 53
d. Cix)= 4.90x - 53​

Answer 1

The answer is b

Explanation:

C(x)=40.60x + 201

Answer 2

Hello!

The answer is:

The second option,

b.)
`C(x)=40.60x+201`

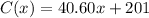
Why?

We are given the functions E(x) and K(x), since they both are function of the same variable, we need to add them in order to find the correct option.

From the statement we know the functions:

`E(x)=22.75x+74`

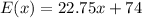
and

`K(x)=17.85x+127`

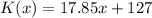
So, adding the functions we have:

`C(x)=E(x)+F(x)`

`C(x)=(22.75x+74)+(17.85x+127)`

`C(x)=22.75x+17.85x+74+127`

`C(x)=40.60x+201`

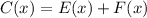
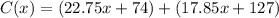
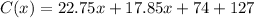
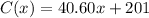
Hence, the answer is the second option,

b.)
`C(x)=40.60x+201`

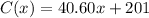
Have a nice day!