Question

What are the domain and range of f(x) =(1/6)^x + 2?

A.domain: x > - 1/6 ; range: y > 0

B.domain: x ; range: y > 2

C.domain: x is a real number; range: y > 2

D.domain: x ; range: y

Answer 1

`\large\boxed{C.\ domain:\ \{x\ |\ x\ \text{is a real number}\};\ range:\ \y\ }`

Explanation:

`f(x)=\left((1)/(6)\right)^x+2\\\\\text{The domain:}\ x\in\mathbb{R}\to\{x\ |\ x\ \text{is a real number\}}\\\\\lim\limits_(x\to\infty)\bigg[\left((1)/(6)\right)^x+2\bigg]=\lim\limits_(x\to\infty)\left((1)/(6)\right)^x+\lim\limits_(x\to\infty)2=0+2=2\\\\\lim\limits_(x\to-\infty)\bigg[\left((1)/(6)\right)^x+2\bigg]=\lim\limits_(x\to-\infty)\left((1)/(6)\right)^x+\lim\limits_(x\to\infty)2=\infty+2=\infty\\\\\text{The range:}\ y\in(2,\ \infty)\to\y\ \\\\\bold{Look\ at\ the\ picture}`

Answer 2

Answer: Option C

domain: x is a real number; range: y

Explanation:

We have the function
`f(x) =((1)/(6))^x + 2`

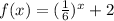
Note that f(x) is an exponential function.

By definition the exponential functions of the form
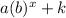`a(b)^x +k` have as domain all real numbers and as range y if
`a>0`,
`b>0`

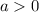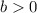
Where a is the main coefficient, b is the base and k is the vertical displacement.

In this case
`k = 2`,
`b=(1)/(6)`,
`a=1`

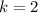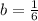Therefore the domain of f(x) is all real numbers and the range of f(x) is

y > 2