Question

Need help!

What is the area of this triangle?
Enter your answer as a decimal in the box round only your final answer to the nearest tenth.

Answer 1

Hello!

The answer is:

The area of the triangle is:

`Area=13.2cm^(2)`

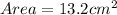
Why?

We can solve the problem using the Side-Angle-Side (SAS) method, to calculate the area of a triangle given two sides and a single angle.

The SAS method to calculate the area of a triangle is given by the following the equation:

`Area=(abSinC)/(2)`

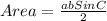
Where,

a and b are the known sides.

C is the known angle

Now, we are given a triangle with the following dimension:

`Side_(a)=7cm\\Side_(b)=8cm\\\alpha=28\°`

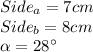
Then, using the information and solving we have:

`Area=(7cm*8cm*Sin(28\°))/(2)`

`Area=(56cm^(2)*Sin(28\°))/(2)\\\\Area=(56cm^(2)*0.47)/(2)\\\\Area=(26.32cm^(2))/(2)\\\\Area=13.16cm^(2)`

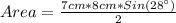
Hence, the area of the triangle, rounded to the nearest tenth is:

`Area=13.2cm^(2)`

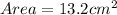
Have a nice day!