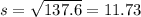Answer:
1. Range =30
2. Variance =137.6
3. Standard deviation=11.7303
Explanation:
This question requires you to find the range, variance and standard deviation of sample data set.
Given the data as; 127 150 121 120 140 128
Arrange the data in ascending order;
sample set S={120, 121, 127, 128, 140, 150}
number of elements, n=6
1. Range = Maximum (S) - Minimum (S) = 150- 120 = 30
⇒Find the mean of the data set
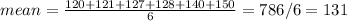
2. Variance is the measure of how far a set of data is spread out.Standard deviation is the square-root of variance.To find variance you need to follow the steps below;
- Find the mean of the sample data
- Find the deviation of each of the data from the mean
- Square each value of the deviations from the mean
- Find the sum in the values of the squared deviations
- Divide the sum in the values of the squared deviations by n-1 where n is the number of elements to get the variance
- Find the square-root of the variance to get the standard deviation of the sample data
Finding the deviations from the mean and their squares
Deviations Squares of deviations
120-131= -11 -11²= 121
121-131= -10 -10² =100
127-131= -4 -4² = 16
128-131= -3 -3= 9
140-131= 9 9²= 81
150-131= 19 19²= 361
Finding the sum of the squares of the deviations from the mean
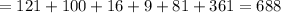
Finding the variance
Variance, S²=(sum of squares of deviations from mean)/ n-1
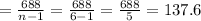
Finding standard deviation
Standard deviation , s , is the square-root of the variance