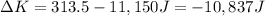Question

A 22.3-g bullet moving at 1 000 m/s is fired through a one-kg block of wood emerging at a speed of 100 m/s. What is the change in the kinetic energy of the bullet-block system as a result of the collision assuming the block is free to move?

Answer 1

-10837 J

Step-by-step explanation:

The law of conservation of momentum states that the initial total momentum is equal to the final total momentum, so:

`p_i = p_f\\m u_b + M u_B = m v_b + M v_B`

where

m = 22.3 g = 0.0223 kg is the mass of the bullet

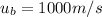`u_b = 1000 m/s` is the initial velocity of the bullet

M = 1 kg is the mass of the block

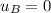`u_B = 0` is the initial velocity of the block

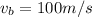`v_b = 100 m/s` is the final velocity of the bullet

`v_B` is the final velocity of the block

Solving for
`v_B` we find

`v_B = (m u_b-m v_b)/(M)=((0.0223 kg)(1000 m/s)-(0.0223 kg)(100 m/s))/(1 kg)=20.1 m/s`

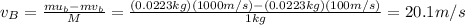
The total kinetic energy before the collision is:

`K_i = (1)/(2)mu_b^2 = (1)/(2)(0.0223 kg)(1000 m/s)^2=11,150 J`

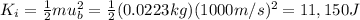
And the total kinetic energy after the collision is:

`K_f = (1)/(2)mv_b^2 + (1)/(2)mv_B^2=(1)/(2)(0.0223 kg)(100 m/s)^2 + (1)/(2)(1 kg)(20.1 m/s)^2=313.5 J`

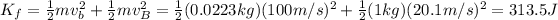
So, the change in kinetic energy is

`\Delta K = 313.5 - 11,150 J = -10,837 J`