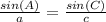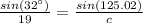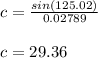Question

Solve the triangle.
A = 32°, a = 19, b = 14

Answer 1

A = 32°, a = 19, b = 14, B=22.98°, C = 125.02°, c = 29.36

Explanation:

We have two sides of the triangle and we have an angle.

A = 32 °, a = 19, b = 14

We use the sine theorem to find the angle B.

We know that according to the sine theorem it is true that:

`(sin(A))/(a)=(sin(B))/(b)=(sin(C))/(c)`

`(sin(32\°))/(19)=(sin(B))/(14)`

`sin(B)=14*(sin(32\°))/(19)\\\\B=Arcsin(14*(sin(32\°))/(19))\\\\B=22.98\°`

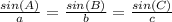
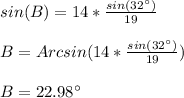
We know that the sum of the internal angles of a triangle is always equal to 180.

So:

`C=180-32-22.98\\\\C=125.02\°`

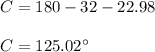
Finally we find the c side

`(sin(A))/(a)=(sin(C))/(c)`

`(sin(32\°))/(19)=(sin(125.02))/(c)`

`0.02789=(sin(125.02))/(c)`

`c=(sin(125.02))/(0.02789)\\\\c=29.36`