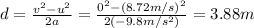(a) 9.8 m/s^2, downward
There is only one force acting on the ball while it is in flight: the force of gravity, which is
F = mg
where
m is the mass of the ball
g is the gravitational acceleration
According to Newton's second law, the force acting on the ball is equal to the product between the mass of the ball and its acceleration, so
F = mg = ma
which means
a = g
So, the acceleration of the ball during the whole flight is equal to the acceleration of gravity:
g = -9.8 m/s^2
where the negative sign means the direction is downward.
(b) v = 0
Any object thrown upward reaches its maximum height when its velocity is zero:
v = 0
In fact, at that moment, the object's velocity is turning from upward to downward: that means that at that instant, the velocity must be zero.
(c) 8.72 m/s, upward
The initial velocity of the ball can be found by using the equation:
v = u + at
Where
v = 0 is the velocity at the maximum height
u is the initial velocity
a = g = -9.8 m/s^2 is the acceleration
t is the time at which the ball reaches the maximum height: this is half of the time it takes for the ball to reach again the starting point of the motion, so
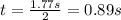
So we can now solve the equation for u, and we find:
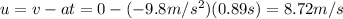
(d) 3.88 m
The maximum height reached by the ball can be found by using the equation:

where
v = 0 is the velocity at the maximum height
u = 8.72 m/s is the initial velocity
a = g = -9.8 m/s^2 is the gravitational acceleration
d is the maximum height reached
Solving the equation for d, we find