Question

The speed of a tennis ball that is served is 73.14 m/s. During a serve, the ball typically starts from rest and is in contact with the tennis racquet for 30 milliseconds. Assuming constant acceleration, what is the average force exerted on the tennis ball during the serve, expressed in terms of the ball’s weight w?

450w
150w
250w
350w

Answer 1

Answer: Third option

F = 250w

Step-by-step explanation:

The impulse can be written as the product of force for the time interval in which it is applied.

`I = F (t_2-t_1)`

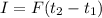
You can also write impulse I as the change of the linear momentum of the ball

`I = mv_2 -mv_1`

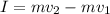
So:

`F (t_2-t_1) = mv_2 -mv_1`

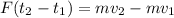
We want to find the force applied to the ball. We know that

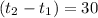`(t_2-t_1) = 30` milliseconds = 0.03 seconds

The initial velocity
`v_1` is zero.

The final speed
`v_2 = 73.14\ m / s`

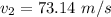
So

`F * 0.03 = 73.14m`

`F * 0.03 = 73.14m\\\\F=(73.14m)/(0.03)\\\\F=2438m`

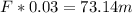
We must express the result of the force in terms of the weight of the ball.

We divide the expression between the acceleration of gravity

`g = 9.8\ m / s ^ 2`

`F=(2438m*g)/(g),\ \ m*g=w\\\\g=9.8\ m/s^2\\\\F=(2438w)/(9.8)\\\\F=249w`

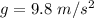
The answer is the third option