Answer:
309 ft
Explanation:
In order to solve this I have to assume that the sling shot is ground level. Since you did not provide an initial height, without making the assumption that it is 0, we cannot solve the problem at all.
The standard form of a quadratic function is
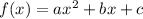
c is the initial height for which we are going to sub in a 0. Given 2 points, we are going to plug in the y and the x, one point each into 2 quadratic functions, to find the model. The first coordinate is (1, 121):
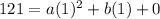 and 121 = a + b
and 121 = a + b
The second coordinate is (2, 224):
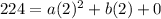 and 224 = 4a + 2b
and 224 = 4a + 2b
Solve the first equation for a:
a = 121 - b
and sub it in for a in the second equation:
224 = 4(121 - b) + 2b and
224 = 484 - 4b + 2b and
-260 = -2b so b = 130.
Now we can sub that in for b and solve for a:
a = 121 - 130 so a = -9.
The equation then that models the motion is
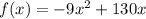
Now that we know that, all we have to do now is to find f(3):
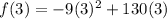 and
and
f(3) = 309 ft