Question

This composite shape is a rectangle with a semicircle attached on one end. The diameter of the semicircle is 6 feet.

What is the approximate area of this composite figure? Use 3.14 for pi and round to the nearest whole number.
46 ft2
74ft2
88 ft2
117ft2

Answer 1

B

Explanation:

Answer 2

As we can see on the picture we have a rectangle and half of circle.

The areas for half circle and rectangle are:

`</p><p>A_(rectangle)=a\cdot b \\</p><p>A_(halfcircle)=(A_(circle))/(2)=(\pi r^2)/(2)</p><p>`

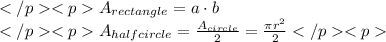
The area of the figure is the sum of the area of half circle and rectangle. Also the height of a rectangle (6ft) is a diameter of a half circle therefore the radius of half circle is 6ft ÷ 2 = 3ft.

Now we calculate the areas.

`</p><p>A_(rectangle)=10\cdot 6=\underline{60} \\</p><p>A_(halfcircle)=(3.14\cdot3^2)/(2)=\underline{14.13} \\</p><p>A_(total)=A_(rectangle)+A_(halfcircle) =60+14.13=\boxed{74.13\approx74}</p><p>`

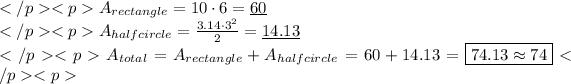
The area of the figure is approximately 74ft squared.

Hope this helps.

r3t40