Question

The number of books borrowed from a library each week follows a normal distribution. When a sample is taken for several weeks, the mean is found to be 190 and the standard deviation is 30.

There is a % chance that more than 250 books were borrowed in a week.

Answer 1

There is a 2.275% chance that more than 250 books were borrowed in a week.

Explanation:

Let the random variable X denote the number of books borrowed from the library each week. Then from the information given;

X is normally distributed with a mean of 190 and a standard deviation of 30.

We are required to determine the probability that more than 250 books were borrowed in a week;

This can be written symbolically as;

Pr(X > 250)

The first step is to determine the z-score associated with the value 250. This is obtained via standardizing X;

Pr(X > 250) =
`Pr(Z>(250-190)/(30))=Pr(Z>2)`

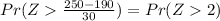
This is simply the area to the right of 2 in a standard normal curve. From the standard normal table, this area is; 0.02275

As a percentage this is equivalent to 2.275%