Question

Jeanne babysits for $6 per hour. She also works as a reading tutor for $10 per hour. She is only allowed to work 20 hours per week. This week, her goal is to make at least $75.

A. Use a system of inequalities to model the scenario above. Let x represent babysitting hours and y represent tutoring hours.
B. Use the model created in part A to create a graph representing Jeanne’s probable income earned and possible number of hours worked this week.
C. Analyze the set of coordinate values that represent solutions for the model created in part A. Choose one of the coordinates within the solution and algebraically prove that the coordinate represents a true solution for the model.

Answer 1

A. We know that
`x` represents babysitting hours and
`y` represent tutoring hours.

Since she is allowed to work 20 hours per week, her babysitting hours plus her tutoring hours can't be more than 20 hours, in other words:

`x+y\leq 20`

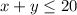
She babysits for $6 per hour and tutor for $10 per our. Since she wants to make at least $75, the sum of babysit hours and tutoring hours must be greater or equal $75, in other words:

`6x+10y\geq 75`

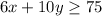
Now we can put our inequalities together to create our system of inequalities:

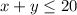`x+y\leq 20` (1)

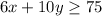`6x+10y\geq 75` (2)

B. To graph our system, we first need to find the equations of the lines bounding the inequalities. To do it we, are replacing the inequality sign with and equal and solving for
`y` in both inequalities.

For
`x+y\leq 20`

`x+y=20`

`y=20-x`

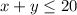
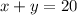
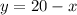
Now we can find the y and x intercepts to graph the line.

The y-intercept occurs when x = 0, so

`y=20-0`

`y=20`

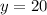
The y-intercept has coordinates (0, 20)

The x-intercept occurs when y = 0, so

`0=20-x`

`-20=-x`

`x=20`

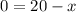
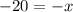
The x-intercept has coordinates (20, 0)

For
`6x+10y\geq 70`

`6x+10y=75`

`10y=75-6x`

`y=(15)/(2)-(3)/(5) x`

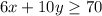
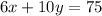
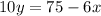
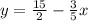
When x = 0,

`y=(15)/(2)-(3)/(5) (0)`

`y=(15)/(2)`

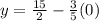
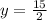
y-intercept =
`(0,(15)/(2))`

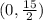
When y = 0,

`0=(15)/(2)-(3)/(5) x`

`-(15)/(2)=-(3)/(5)x`

`x=-(15)/(2)(-(5)/(3) )`

`x=(25)/(2)`

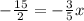
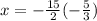
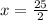
x-intercept =
`((25)/(2) ,0)`

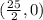
Now, since both inequalities have greater or equal/less or equal signs, the line bounding them are solid.

Now we can put it all together to create the graph of our system (check the attached picture).

The solution of the inequality is the shaded (purple) region where the two inequalities intercept.

C. As we can see in the graph the points (10, 5), (5, 8), and (2, 9) -as well as the x and y intercepts of both inequalities, are solutions of the system.

Let's choose the point (10, 5). To prove algebraically that the point is a valid solution of the system, we just need to replace the values in our system of inequalities and prove that both inequalities are true.

Since the point is (10, 5), x = 10 and y = 5

Replacing values in (1)

`x+y\leq 20`

`10+5\leq 20`

`15\leq 20`

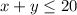
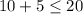
Since 15 is indeed less or equal to 20, the inequality is true.

Replacing values in (2)

`6x+10y\geq 75`

`6(10)+10(5)\geq 75`

`60+50\geq 75`

`110\geq 75`

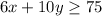
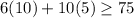
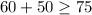
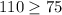
Since 110 is greater or equal 75, the inequality is true.

Both inequalities are true, so (10, 5) represents a solution for the model.