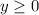Question

John is at a local bait shop; he wants to buy bait for his fishing trip. At the store, they are selling live bait for $12 a pound and natural bait for $7 a pound. John would like to get at least 3 pounds of live bait, but he only has a budget of $63. Let x be the amount of live bait and y be the amount of natural bait. Model the scenario with a system of inequalities.

Answer 1

`x\geq3`

`12x+7y\leq63`

`y\geq0`

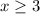
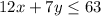
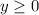
Explanation:

If we let x be the amount of live bait and y be the amount of natural bait, Then we can come up with the following inequalities;

We are told that John would like to get at least 3 pounds of live bait. At least 3 means 3 or more. Since x represents the amount of live bait, we have;

`x\geq3`

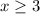
Moreover,we are informed that;

The store sells live bait for $12 a pound and natural bait for $7 a pound. x pounds of live bait would cost 12x while y pounds of natural bait would cost 7y. The total cost would thus be;

12x + 7y

but John only has a budget of $63. This implies that he can spend $63 at most, thus;

`12x+7y\leq63`

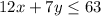
Finally we can have our last inequality as;

`y\geq0`