Answer:
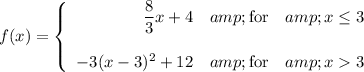
Explanation:
The line to the left of x=3 goes up from 4 to 12 as x goes from 0 to 3. Thus, the slope of it is ...
slope = (12 -4)/(3 -0) = 8/3
It intersects the y-axis at y=4, so its equation is ...
y = (8/3)x +4
__
For x > 3, we observe that the curve falls 3 units (from 12 to 9) as x goes from 3 to 4, then falls 9 units (from 9 to 0) as x goes from 4 to 5. The slope of the curved portion at x=3 looks like it might be zero, suggesting a polynomial function instead of an exponential function.
We note that the change in the value of y=x^2 as x goes from 0 to 1 is 1, then as x goes from 1 to 2, it is 4-1 = 3 — 3 times the change in the first interval. This suggests a quadratic function that has been scaled by a vertical factor of -3, and had its vertex moved to (3, 12). Such a function is described by ...
y = -3(x -3)² +12
Then the graph is modeled by a piecewise function, defined as a line for x < 3, and as a quadratic curve for x > 3. Since the function is continuous at x=3, we can put "or equal to" signs on either or both of these boundaries. We choose to write it as ...
f(x) = (8/3)x +4, x ≤ 3; -3(x -3)² +12, x > 3.
____
The graph of our function is attached. It substantially matches the given graph.