Question

Find the Quadratic function y=a(x-h)^2 who's graph passes through the given points (4,-2) and (2,0)

Answer 1

Given:

The graph passes through the given points (4,-2) and (2,0).

To find:

The quadratic function
`y=a(x-h)^2`.

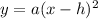Solution:

We have, quadratic function

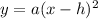`y=a(x-h)^2` ...(i)

The graph passes through the given points (4,-2) and (2,0). It means the equation must be true for these points.

Putting x=4 and y=-2 in (i), we get

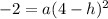`-2=a(4-h)^2` ...(ii)

Putting x=2 and y=0 in (i), we get

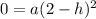`0=a(2-h)^2` ...(iii)

Divide (iii) by (ii).

`(0)/(-2)=(a(2-h)^2)/(a(4-h)^2)`

`0=((2-h)^2)/((4-h)^2)`

`0=(2-h)^2`

`0=2-h`

`h=2`

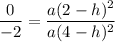
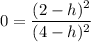
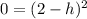
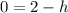
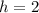
Putting h=2 in (ii), we get

`-2=a(4-2)^2`

`-2=a(2)^2`

`-2=a(4)`

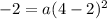
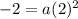
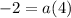
Divide both sides by 4.

`(-2)/(4)=a`

`(-1)/(2)=a`

Putting
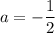`a=-(1)/(2)` and h=2 in (i), we get

`y=-(1)/(2)(x-2)^2`

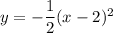
Therefore, the required quadratic function is
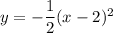`y=-(1)/(2)(x-2)^2`.