Answer:
Correct choice is A.
Explanation:
Given functions are
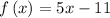 and
and
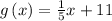 .
.
Then
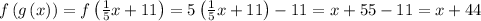
By definition of inverse we says that if f(x) and g(x) are inverse of each other then f(g(x)) must be equal to x.
But in above calculation we can see that f(g(x)) is not equal to x.
Hence correct choice is A.