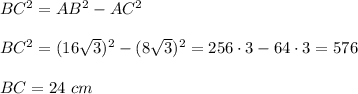Question

In right △ABC, the altitude CH to the hypotenuse AB intersects angle bisector AL in point D. Find the sides of △ABC if AD = 8 cm and DH = 4 cm.

Answer 1

`AC=8√(3)\ cm\\ \\AB=16√(3)\ cm\\ \\BC=24\ cm`

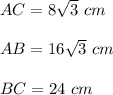
Explanation:

Consider right triangle ADH ( it is right triangle, because CH is the altitude). In this triangle, the hypotenuse AD = 8 cm and the leg DH = 4 cm. If the leg is half of the hypotenuse, then the opposite to this leg angle is equal to 30°.

By the Pythagorean theorem,

`AD^2=AH^2+DH^2\\ \\8^2=AH^2+4^2\\ \\AH^2=64-16=48\\ \\AH=√(48)=4√(3)\ cm`

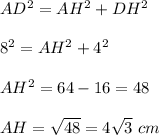
AL is angle A bisector, then angle A is 60°. Use the angle's bisector property:

`(CA)/(CD)=(AH)/(HD)\\ \\(CA)/(CD)=(4√(3))/(4)=√(3)\Rightarrow CA=√(3)CD`

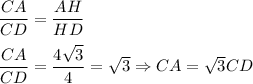
Consider right triangle CAH.By the Pythagorean theorem,

`CA^2=CH^2+AH^2\\ \\(√(3)CD)^2=(CD+4)^2+(4√(3))^2\\ \\3CD^2=CD^2+8CD+16+48\\ \\2CD^2-8CD-64=0\\ \\CD^2-4CD-32=0\\ \\D=(-4)^2-4\cdot 1\cdot (-32)=16+128=144\\ \\CD_(1,2)=(-(-4)\pm√(144))/(2\cdot 1)=(4\pm 12)/(2)=-4,\ 8`

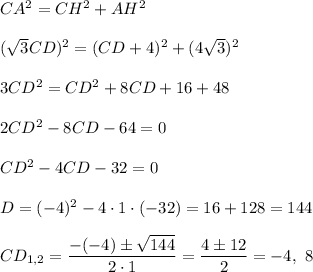
The length cannot be negative, so CD=8 cm and

`CA=√(3)CD=8√(3)\ cm`

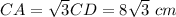
In right triangle ABC, angle B = 90° - 60° = 30°, leg AC is opposite to 30°, and the hypotenuse AB is twice the leg AC. Hence,

`AB=2CA=16√(3)\ cm`

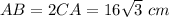
By the Pythagorean theorem,

`BC^2=AB^2-AC^2\\ \\BC^2=(16√(3))^2-(8√(3))^2=256\cdot 3-64\cdot 3=576\\ \\BC=24\ cm`