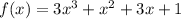Question

write a polynomial function of least degree with integral coefficients that has the given zeros. -(1/3), -i

Answer 1

`f(x)=3x^3+x^2+3x+1`

Explanation:

If a real number
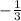`-(1)/(3)` is a zero of polynomial function, then

`x-\left(-(1)/(3)\right)=x+(1)/(3)`

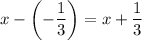
is the factor of this function.

If a complex number
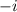`-i` is a xero of the polynomial function, then the complex number
`i` is also a zero of this function and

`x-(-i)=x+i\ \text{ and }\ x-i`

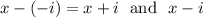
are two factors of this function.

So, the function of least degree is

`f(x)=\left(x+(1)/(3)\right)(x+i)(x-i)=\left(x+(1)/(3)\right)(x^2-i^2)=\\ \\ =\left(x+(1)/(3)\right)(x^2+1)=(1)/(3)(3x+1)(x^2+1)=(1)/(3)(3x^3+x^2+3x+1)`

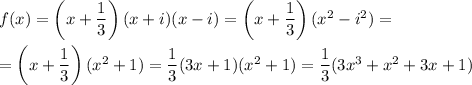
If the polynomial function must be with integer coefficients, then it has a form

`f(x)=3x^3+x^2+3x+1`