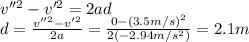Question

A 0.0240 kg bullet moving horizontally at 400 m/s embeds itself into an initially stationary 0.500 kg block.

(a) What is their velocity (in m/s) just after the collision? m/s
(b) The bullet-embedded block slides 8.0 m on a horizontal surface with a 0.30 kinetic coefficient of friction. Now what is its velocity (in m/s)? m/s
(c) The bullet-embedded block now strikes and sticks to a stationary 2.00 kg block. How far (in m) does this combination travel before stopping? m

Answer 1

(a) 18.3 m/s

According to the law of conservation of momentum, the total initial momentum of the system must be equal to the total final momentum, so we have

`p_i = p_f\\m u = (m+M)v`

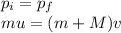
where

m = 0.0240 kg is the mass of the bullet

u = 400 m/s is the initial speed of the bullet

M = 0.5 kg is the mass of the block

v is the final speed of the block+bullet together

Solving for v, we find the velocity after the collision

`v=(mu)/(m+M)=((0.0240 kg)(400 m/s))/(0.0240 kg+0.5 kg)=18.3 m/s`

(b) 17.0 m/s

The frictional force acting on the bullet-block system is

`F_f = -\mu (m+M)g`

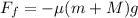
where

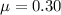`\mu = 0.30` is the coefficient of kinetic friction

The acceleration due to the frictional force, therefore, will be equal to the frictional force divided by the total mass:

`a=(F_f)/(m+M)=\-mu g = -(0.30)(9.8 m/s^2)=-2.94 m/s^2`

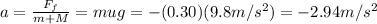
The system travels for a distance of

d = 8.0 m

So we can find the final velocity using the equation:

`v_f^2 = v^2 + 2ad`

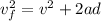
where

v = 18.3 m/s is the initial velocity, found at point a). Substituting,

`v_f = √((18.3 m/s)^2+2(-2.94 m/s^2)(8.0 m))=17.0 m/s`

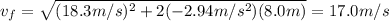
(c) 2.1 m

We can use again the law of conservation of momentum:

`(m+M) v = (m+M+M')v'`

where

v = 17.0 m/s is the initial velocity of the initial bullet+block system

M = 2.00 kg is the mass of the second block

v' is the final velocity of the system

Solving for v',

`v=((m+M)v)/(m+M+M')=((0.0240 kg+0.5 kg)(17.0 m/s))/(0.0240 kg+0.5 kg+2.00 kg)=3.5 m/s`

The acceleration of the system on the rough surface is still

`a=-2.94 m/s^2`

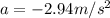
So we can find the distance covered by using again the formula used before, and requiring that the final velocity should be zero (v''=0):

`v''^2 - v'^2 = 2ad\\d=(v''^2-v'^2)/(2a)=(0-(3.5 m/s)^2)/(2(-2.94 m/s^2))=2.1 m`