Answer:
Town C is approximately 58.356 kilometers from town A.
Explanation:
According to the statement, we understand that tourist travels from town A to town B (50 kilometers) at a direction of 80º west of north and from town B to town C (40 kilometers) at a direction of 20º east of north. Vectorially speaking, the resultant from town A to town C is described by the following formula:
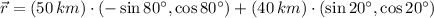
![\vec r = (-35.560,46.270)\,[km]](https://img.qammunity.org/2022/formulas/mathematics/high-school/in5rq7zro4sfqpslpgriwjwmxvawssrx98.png)
The distance from town A to town C is the magnitude of vector reported above, which is now calculated by Pythagorean Theorem:
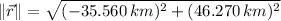
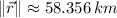
Town C is approximately 58.356 kilometers from town A.