Answer:
The correct options are 1 and 3.
Explanation:
From the given box plot it is clear that
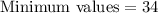
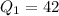
Q₁ is 25% of a data.
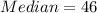
Median is 50% of a data.
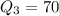
Q₃ is 75% of a data.
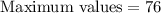
34 is minimum value of the data and 46 is median it means 50% of the data values lies between 34 and 46. Therefore option 1 is correct.
42 is first quartile and and 70 is third quartile. it means 50% of the data values lies between 42 and 70. Therefore option 2 is incorrect.
The difference between Minimum value and first quartile, Maximum value and third quartile is less than 1.5×(IQR), therefore it is unlikely to have any outliers in the data.
Hence option 3 is correct.
The interquartile range of the data is
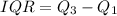

The interquartile range is 28. Therefore option 4 is incorrect.
Range of the data is

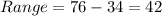
The range is 42. Therefore option 5 is incorrect.