Answer:
The line x = 8 is our vertical asymptote
The limit of
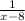 as x approaches 8 from the left is negative infinity; -∞
as x approaches 8 from the left is negative infinity; -∞
Explanation:
We have been given the following function;
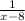
Considering that the function is rational, it will defined everywhere on the real line except where the expression in the denominator will be 0;
That is the function will not be defined where;
x - 8 = 0
solving for x yields;
x = 8
The function will be approaching the vertical line x = 8 asymptotically, meaning that the function will never touch or cross this line. We can therefore say that,
The line x = 8 is our vertical asymptote for the given function
The limit of
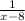 as x approaches 8 from the left;
as x approaches 8 from the left;
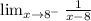
For x approaching 8 from the left,
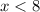 which implies that
which implies that
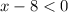
The denominator will be a negative quantity approaching 0 from the left, that is -∞.
Thus;
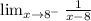 = -∞
= -∞
Find the graph attached.