Question

John, Rick, and Molli can paint a room working together in 6 hours. Alone, John can paint the room in 12 hours. If Rick works alone, he can paint the room in 15 hours. Write an equation comparing the group rate to the sum of the individual rates. Then find how long it will take Molli to paint the room if working alone.

Answer 1

`(1)/(12)+(1)/(15)+(1)/(x)=(1)/(6)`

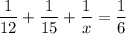
60 hours

Explanation:

John - 12 hours

Rick - 15 hours

Molli - x hours

Together - 6 hours

Each of them can paint:

John -
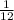`(1)/(12)` of a room per hour

Rick -
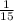`(1)/(15)` of a room per hour

Molli -
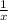`(1)/(x)` of a room per hour

Together -
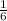`(1)/(6)` of a room per hour

So the equation is

`(1)/(12)+(1)/(15)+(1)/(x)=(1)/(6)`

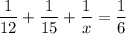
Solve this equation:

`(1)/(x)=(1)/(6)-(1)/(12)-(1)/(15)\\ \\(1)/(x)=(10-5-4)/(60)=(1)/(60)\\ \\x=60`

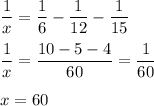
Molli can paint the room in 60 hours.