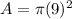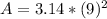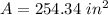Marcy is making a hooked circle-shaped rug for her mother. The circumference of the circle-shaped rug is 56.52 inches. What is the area of the rug? Use = 3.14.

Question

asked Apr 9, 2020 198k views

1 Answer

Norrisa · Answer 1 · 2020-04-14T03:12:04+0000

Answer:

The area is

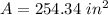
$A=254.34\ in^2$

Explanation:

The circumference of a circle is given by a following formula:

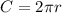
$C = 2\pi r$

Where r is the radius of the circumference.

In this case we know that

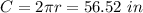
$C = 2\pi r=56.52\ in$

We solve the equation for r

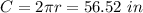
$C = 2\pi r=56.52\ in$

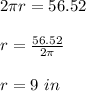
$2\pi r=56.52\\\\r=(56.52)/(2\pi)\\\\r=9\ in$

The area of a circumference is given by the following formula

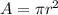
$A=\pi r^2$

Now we substitute the value of r in the equation to find the area

$A=\pi (9)^2$

A=3.14* (9)^2

$A=254.34\ in^2$