Question

The diagonals of quadrilateral ABCD intersect at E (2,5). ABCD has vertices at A (3,7) and B (3,6). What must be the coordinates of Upper C and Upper D to ensure that ABCD is a​ parallelogram?

Answer 1

C(1,3) and D(1,4).

Explanation:

The given quadrilateral ABCD has vertices at A (3,7) and B (3,6). The diagonals of this quadrilateral ABCD intersect at E (2,5).

Recall that, the diagonals of a parallelogram bisects each other.

This means that; E(2,5) is the midpoint of each diagonal.

Let C and D have coordinates C(m,n) and D(s,t)

Using the midpoint rule:

`((x_2+x_1)/(2), (y_2+y_1)/(2))`

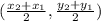
The midpoint of AC is
`((m+3)/(2), (n+7)/(2))=(2,5)`

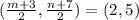
This implies that;

`((m+3)/(2)=2, (n+7)/(2)=5)`

`(m+3=4, n+7=10)`

`(m=4-3, n=10-7)`

`(m=1, n=3)`

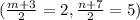
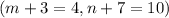
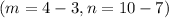
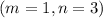
The midpoint of BD is
`((m+3)/(2), (n+7)/(2))=(2,5)`

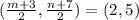
This implies that;

`((s+3)/(2)=2, (t+6)/(2)=5)`

`(s+3=4, t+6=10)`

`(s=4-3, t=10-6)`

`(s=1, t=4)`

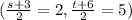
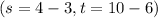
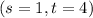
Therefore the coordinates of C are (1,3) and D(1,4).