Answer:
Probability of the sticks weight being 2.44 oz or greater is 0.01017 .
Explanation:
We are given that the manufacturer's website states that the average weight of each stick is 2.00 oz with a standard deviation of 0.19 oz.
Also, it is given that the weight of the drumsticks is normally distributed.
Let X = weight of the drumsticks, so X ~ N(
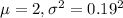 )
)
The standard normal z distribution is given by;
Z =
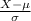 ~ N(0,1)
~ N(0,1)
Now, probability of the sticks weight being 2.44 oz or greater = P(X >= 2.44)
P(X >= 2.44) = P(
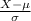 >=
>=
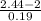 ) = P(Z >= 2.32) = 1 - P(Z < 2.32)
) = P(Z >= 2.32) = 1 - P(Z < 2.32)
= 1 - 0.98983 = 0.01017
Therefore, the probability of the sticks weight being 2.44 oz or greater is 0.01017 .