Answer:
In Geography test student score better relative to the other students in each class.
Explanation:
We are given that a student scores 56 on a geography test and 285 on a mathematics test. The geography test has a mean of 80 and a standard deviation of 20. The mathematics test has a mean of 300 and a standard deviation of 10.
Let X = Student scores in geography test
Y = Student scores in mathematics test
Here, Mean score of geography test,
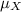 = 80
= 80
Standard deviation of geography test,
 = 20
= 20
Also, Mean score of mathematics test,
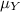 = 300
= 300
Standard deviation of mathematics test,
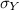 = 10
= 10
For comparing on which test did the student score better relative to the other students in each class we will find the z score of both the test as data for both tests are normally distributed;
Z =
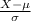 ~ N(0,1)
~ N(0,1)
- Z score for geography test,
 ;
;
 =
=
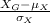 =
=
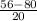 = -1.2
= -1.2
- Z score for mathematics test,
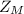 ;
;
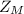 =
=
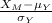 =
=
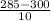 = -1.5
= -1.5
From both the z scores it is clear that z score of geography test is higher than that of mathematics test.
Therefore, the student score better relative to the other students in each class in geography test .