Question

G(x) = x^3 - x^2 - 4x + 4 what are the zeros, the y-intercept and the end behavior.

I think it's -2,0 1,0 2,0 for the zeros
y-intercept 0,4 but i'm not sure about them and have no clue about the end behavior

Answer 1

The zeros: x = 1, -2, 2

The y-intercept: (0, 4)

The end behavior :

x --> + ∞, f(x) --> + ∞

x --> - ∞, f(x) --> - ∞

Explanation:

Zero function:

x^3 - x^2 - 4x + 4 = 0

(x^3 - x^2) - (4x - 4) = 0

x^2(x - 1) - 4(x - 1) = 0

(x^2 - 4)(x - 1) = 0

(x + 2)(x - 2)(x - 1) = 0

x + 2 = 0; x = -2

x - 2 = 0; x = 2

x - 1 = 0; x = 1

The zeros: x = 1, -2, 2

The y-intercept when x = 0 so y-intercept = 4 or (0, 4)

The end behavior of a function f(x) : the behavior of the graph of the function at the ends of the x-axis.

As x approaches + ∞, f(x) approaches + ∞

As x approaches - ∞, f(x) approaches - ∞

Answer 2

See explanation

Explanation:

Zeros of the function are those values of x, for which g(x)=0, so solve the equation g(x)=0:

`x^3-x^2-4x+4=0\\ \\x^2(x-1)-4(x-1)=0\\ \\(x-1)(x^2-4)=0\\ \\(x-1)(x-2)(x+2)=0\\ \\x_1=-2,\ x_2=1,\ x_3=2`

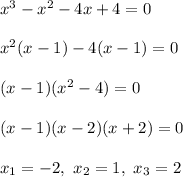
Hence, the function has three zeros, x=-2, x=1 and x=2.

To find the y-intercept, substitute x=0:

`y=g(0)=0^3-0^2-4\cdot 0+4=4,`

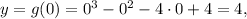
so y-intercept is at point (0,4).

The graph of the function shows that when x is infinitely small, then y is infinitely small too and if x is infinitely large, then y is infinitely large too.