Question

Find the median, first quartile, third quartile, interquartile range, and any outliers for each set of data.

14.6, 28.1, 3.9, 7.1, 5.3, 30.9, 2.8, 6.5, 20.8, 16.4, 16.4, 27.1, 53.5, 12.5, 6.1

Answer 1

Here is what i figured out.

Answer 2

First, to find the median, we have to order all numbers, from least to highest:

2.8; 3.9; 5.3; 6.1; 6.5; 7.1; 12.5; 14.6; 16.4; 16.4; 20.8; 27.1; 28.1; 30.9; 53.5

Now, we calculate the position of each quartile:

`Q_(k)=(k(n+1))/(4)\\Q_(1)=(1(15+1))/(4)=4\\Q_(2)=(2(15+1))/(4)=8\\Q_(3)=(3(15+1))/(4)=12`

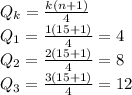
So, the first quartile is in the fourth position, the thirds quartile is in the twelfth position:

So, first quartile is 6.1. Second quartile is 14.6, and the third quartile is 27.1.

It's important to remember that the second quartile is the median. So the median is 14.6

Lastly, the interquartile range is the difference between the third and first quartile. So:

`Q_(3)-Q_(1)=27.1-6.1=21`

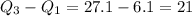
Therefore, the interquartile range is 21.