Answer:
Reasonable domain is [1.375,3].
Explanation:
Given function is
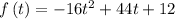 .
.
Now we need to find about what is the reasonable domain of the graph of the function
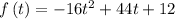 when the basketball falls from its maximum height to the ground.
when the basketball falls from its maximum height to the ground.
Compare with
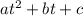 , we get a=-16 and b=44
, we get a=-16 and b=44
then t-coordinate of vertex
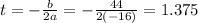
Then that means maximum height of the ball occurs when time t=1.375 seconds.
Now let's find time when ball falls on ground so set f(t)=0
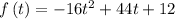

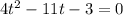
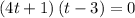
 or
or
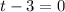
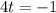 or
or
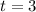
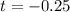 or
or
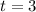
Time can't be negative so we use t=3 only
Hence reasonable domain is [1.375,3].