Answer:
Company 1 is greater.
Explanation:
Given,
The function that shows the production cost of company 1,
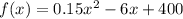
Differentiating with respect to x,
We get,
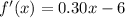
Again differentiating,
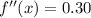
For minimum or maximum,
f'(x) = 0,
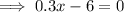
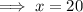
Since, at x = 20, f''(x) = Positive,
So, f(x) is minimum at x = 20,
⇒ Minimum cost in company 1 is,
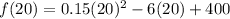
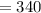
Also, by the given table,
The minimum cost of company 2 is at x = 70,
g(70) = 55,
Since, 340 > 55,
Hence, Based on the given information, the minimum production cost for company 1 is greater.